Statistics and Probability

For the booklet on statistics and probability, click here

Class Data - Am I Average?

To access the classes data that we collected on Thursday, click here

Reminder about test

Just a reminder that our test for Algebra is on tomorrow (Tuesday 1st December). You will be allowed an A5 single sided information sheet, as well as a calculator in the test. Your assignment are also due on Tuesday the 1st of December if they are not already handed in.

Assignment

We have finished off this unit on Algebra. I have uploaded an assignment for this into the "Assignments" tab. This assignment will be due on Friday the 27th of November.

We will be having a test on this unit, but stay posted for more details on this.

If you have any questions feel free to comment on this post, or email or chat to me in person.

Solving Equations

We are nearing the end of our unit on Algebra. We are now looking at solving equations. When I say solving equations, what I really mean is coming up with a value for our pronumeral (i.e. our letter in an equation).
Firstly, we need to know what an equation is. An equation is really a mathematical sentence where "something" is equal to "something else". So for example, we may have an equation like so;

5x - 6 = 14

This satisfies the definition for an equation because we have "something" (5x - 6) being equal tp "something else" (14). Now if we wanted to solve this, we want to come up with a value for "x" that makes this equation true (i.e. a number we can substitute in for "x" that makes 5x - 6 equal to 14). 

We can do this a few ways. One way is simply using trial and error. We can try values for x, and hope we come up with a result. This can work sometimes, but when equations get very complicated this method falls down. 

Another method is called the "back-tracking method". This method is a little more complicated, but it will work every time. Once you get the hang of it, it works really well. 

The back-tracking method involves applying mathematical operations to the equation to try and get out pronumeral by itself on one side of our equal side, and a number on the other side of the equal sign. We do this by back-tracking through the equations that we have, doing the opposite to what the equation is asking us to do. For example, if our equation says to add 4, to solve it we would subtract 4. If our equation says to multiply by  3, we would do the opposite which is dividing by 3. 

Now for more information on this, and some great worked examples, have a look at this document by clicking here.

I have uploaded a worksheet on doing this in the "Worksheets" tab. Work through this. It is a new and quite difficult concept, so take your time with it. Use the examples and explanations in the document above to help you. If you are still having troubles, feel free to comment on this post, or email or chat to me in person. 

The Cartesian Plane

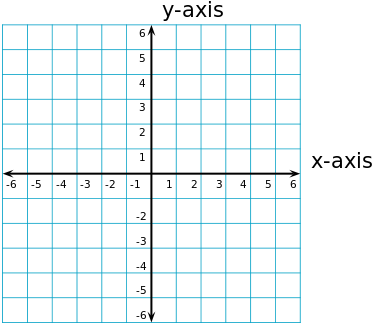
We have recently been doing work on the Cartesian plane. This can be applied to algebra, because when we plot points on the Cartesian plane, we can draw a line through these points then use algebra to create a rule that represents all of the points on this line, not just the points we plotted.

The Cartesian plane is a set of axes, the a-axis and the y-axis. The x-axis runs horisontally and the y-axis runs vertically on the page.

When we plot points on the Cartesian plane, they are written in the following form;

(x, y)

The x represents how far we move in the x-direction (or along the x-axis) and the y represents how far we move in the y-direction (or the y-axis). So a point (4, 5) means we move 4 units in the x-direction (horisontally) and 5 units in the y-direction (vertically). 

I have been very brief with my information here, however the following website is great. It has some really good information and goes into some nice detail, so I defiantly suggest you check that out. 

http://www.mathsisfun.com/data/cartesian-coordinates.html 

I have uploaded a new worksheet on this into the "Work Sheets" folder, so check this out and work through this. 

If you do have any questions on this feel free to comment on this post, or email or chat to me in person. 

Making rules

A common use for algebra is to make rules about certain situations, and using pronumerals and variables to allow these rules to work for a variety of different circumstances. It is important that we understand how to set up these rules. It is quite difficult for me to teach you how to do this using this blog, so what I have done is uploaded some pages from a text book that explain what to do quite well. They have some worked examples as well which are handy to look at.

This document can be found by clicking here. Read through this and use the worked examples to help you work through the new worksheet, which has been uploaded to the "Worksheets" tab. This new worksheet looks like a lot of work, but once you get the hang of it, it will not take you long at all. Make sure you check your answers with the answers provided. I will say that the answer for questions 1 in section 5.5 does have an error in it, but the rest of the answers are correct.

As always, if you have any questions feel free to comment on this post, or email or chat to me in person.