Statistics and Probability

For the booklet on statistics and probability, click here

Class Data - Am I Average?

To access the classes data that we collected on Thursday, click here

Reminder about test

Just a reminder that our test for Algebra is on tomorrow (Tuesday 1st December). You will be allowed an A5 single sided information sheet, as well as a calculator in the test. Your assignment are also due on Tuesday the 1st of December if they are not already handed in.

Assignment

We have finished off this unit on Algebra. I have uploaded an assignment for this into the "Assignments" tab. This assignment will be due on Friday the 27th of November.

We will be having a test on this unit, but stay posted for more details on this.

If you have any questions feel free to comment on this post, or email or chat to me in person.

Solving Equations

We are nearing the end of our unit on Algebra. We are now looking at solving equations. When I say solving equations, what I really mean is coming up with a value for our pronumeral (i.e. our letter in an equation).
Firstly, we need to know what an equation is. An equation is really a mathematical sentence where "something" is equal to "something else". So for example, we may have an equation like so;

5x - 6 = 14

This satisfies the definition for an equation because we have "something" (5x - 6) being equal tp "something else" (14). Now if we wanted to solve this, we want to come up with a value for "x" that makes this equation true (i.e. a number we can substitute in for "x" that makes 5x - 6 equal to 14). 

We can do this a few ways. One way is simply using trial and error. We can try values for x, and hope we come up with a result. This can work sometimes, but when equations get very complicated this method falls down. 

Another method is called the "back-tracking method". This method is a little more complicated, but it will work every time. Once you get the hang of it, it works really well. 

The back-tracking method involves applying mathematical operations to the equation to try and get out pronumeral by itself on one side of our equal side, and a number on the other side of the equal sign. We do this by back-tracking through the equations that we have, doing the opposite to what the equation is asking us to do. For example, if our equation says to add 4, to solve it we would subtract 4. If our equation says to multiply by  3, we would do the opposite which is dividing by 3. 

Now for more information on this, and some great worked examples, have a look at this document by clicking here.

I have uploaded a worksheet on doing this in the "Worksheets" tab. Work through this. It is a new and quite difficult concept, so take your time with it. Use the examples and explanations in the document above to help you. If you are still having troubles, feel free to comment on this post, or email or chat to me in person. 

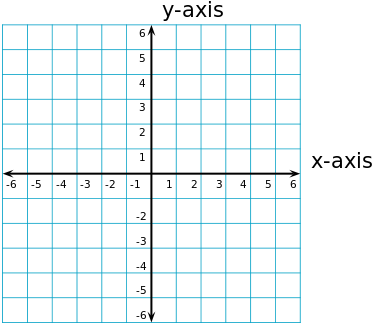
The Cartesian Plane

We have recently been doing work on the Cartesian plane. This can be applied to algebra, because when we plot points on the Cartesian plane, we can draw a line through these points then use algebra to create a rule that represents all of the points on this line, not just the points we plotted.

The Cartesian plane is a set of axes, the a-axis and the y-axis. The x-axis runs horisontally and the y-axis runs vertically on the page.

When we plot points on the Cartesian plane, they are written in the following form;

(x, y)

The x represents how far we move in the x-direction (or along the x-axis) and the y represents how far we move in the y-direction (or the y-axis). So a point (4, 5) means we move 4 units in the x-direction (horisontally) and 5 units in the y-direction (vertically). 

I have been very brief with my information here, however the following website is great. It has some really good information and goes into some nice detail, so I defiantly suggest you check that out. 

http://www.mathsisfun.com/data/cartesian-coordinates.html 

I have uploaded a new worksheet on this into the "Work Sheets" folder, so check this out and work through this. 

If you do have any questions on this feel free to comment on this post, or email or chat to me in person. 

Making rules

A common use for algebra is to make rules about certain situations, and using pronumerals and variables to allow these rules to work for a variety of different circumstances. It is important that we understand how to set up these rules. It is quite difficult for me to teach you how to do this using this blog, so what I have done is uploaded some pages from a text book that explain what to do quite well. They have some worked examples as well which are handy to look at.

This document can be found by clicking here. Read through this and use the worked examples to help you work through the new worksheet, which has been uploaded to the "Worksheets" tab. This new worksheet looks like a lot of work, but once you get the hang of it, it will not take you long at all. Make sure you check your answers with the answers provided. I will say that the answer for questions 1 in section 5.5 does have an error in it, but the rest of the answers are correct.

As always, if you have any questions feel free to comment on this post, or email or chat to me in person.

Like Terms

We are now looking at like terms in algebra.

Firstly, we have to remember what a term is. A term is a number, a pronumeral, or a combination of both of these. For example, 4 is a term, x is a term, and 3abxyz is also a term. When we write an algebraic expression, terms are easy to spot because they are always seperated by a "+" or a "-". For example, in the expression;

2ab + 4c - 6 - x

our terms are 2ab, 4c, -6, and -x.

Now like terms are special terms. These are terms that have EXACTLY the same combination of pronumerals (letters). For example, 2a and 4a are like terms, because they both have just the pronumeral "a". However, 4b and 5bc are NOT like terms. They both do have a "b" in them, however the 5bc also contains a "c" so the combination of pronumerals is different.  

If we have a look at an expression now; 

4a + 2ab + 5 - a + 3ab - 1

We can go and collect like terms in this, so the like terms would be:

• 4a and -a
• 2ab and 3ab
• 5 and -1 

Once we have collected the like terms in an expression, we can do a process called simplification (or simplifying) where we combine these like terms and write the expression in a simpler, shorter way. So again looking at the expression above, if we were to combine the like terms we would get:

• 4a and -a becoming 3a, because we start with 4 lots of a and then take 1 lot of a away, leaving us with 3 lots of a, or 3a. 
• 2ab and 3ab becoming 5ab, because we start with 2 lots of ab and add 3 more lots of ab, leaving us with 5 lots of ab, or 5ab. 
• 5 and -1 becoming 4, because we start with 5 and take 1 away, leaving us with 4. 

We can then write our expression with the combined like terms instead of all of the original terms. The new expression would look like; 

3a + 5ab + 4

Which as you can see is much simpler and much shorter than the previous expression. We have now simplified the expression. 

Now a few points to remember when doing these questions is that when we are looking at these expressions and like terms; 

1. Don't worry about the coefficient (the number out the front of the term, so the 4 in 4ax). When we look at identifying like terms, we are just looking at the pronumerals. Once you have identified the like terms, you can then look at the coefficients and use these to combine your like terms. 
2. The order of the pronumerals does not matter. xy is the same as yx, so 4xy and 3yx would be like terms. If you really think about it, the combination of pronumerals in these terms is still the same. They both have an "x" and they both have a "y", so they must be like terms. 

I have uploaded a worksheet for this into the "Worksheets" tab. Work through this now for class work and homework. The first page is the most important work. The second page contains extra questions to work through if you have time. Remember to check your answers with the answers provided. 

If you have any questions feel free to comment on this post, or email or chat to me in person. 

Intro to Algebra - Continued

We are continuing to introduce Algebra and the processes we follow working with this. Be sure to familiarise yourself with the table of common algebra words and their definitions in the previous post. These are really important to understand, as they are used a lot in Algebra now and in the future.

One common misconception that I have be noticing come in when we are substituting. Substitution is the process where we replace the pronumerals (letters) with number values and actually solve algebraic expressions or equations. So for example, solve;

a + 3, when a = 6

We would simply replace the "a" with the value of 6 and solve, getting;

6 + 3 = 9

The misconception occurs when we have a problem like this. Solve; 

4b, when b = 7

We need to remember when we write 4b, what we are really saying is "4 lots of b" or "4 multiplied by b". This can be confusing, because if we replace the "b" with a 7 in this example, we could think the solution is actually 47, which is incorrect. This is why it is really important to remember that 4b really means "4 lots of b". So the solution for this example would be; 

4 x 7 = 28

You should be able to finish off the first worksheet for this algebra unit, which can be found in the "Worksheets" tab. We do not have maths again till Thursday the 29th of October, so this should give you plenty of time to finish this off. Remember to check your answers as you go. Some of the answers given by this worksheet are incorrect, however these are quite obviously wrong. 

If you have any questions on anything to do with this post or the worksheet, feel free to comment on this post, or email or chat to me in person. 

Introduction to Algebra

We have started a new unit this term. This unit will be on Algebra. When people here the word Algebra they often get quite nervous and think it changes everything in maths, making it heaps harder. This is not the case. Algebra still obeys all of the same laws that standard maths follows. The only difference is we are using symbols to represent information, instead of number like we have previously. The reason we use symbols is because sometimes values or information can change. If we look at the number 4 for example, this can only ever represent one value (4 units). However, if we use symbols, they can be used to represent any value we want. An example could be;

If we want to find the total number of people at the school, we can set up an equation like so;

Total number of people = a + b + c + d

where a = the number of students at school today, b = the number of teachers at school today, c = the number of support staff at school today (i.e. cleaners, office staff, etc), and d = the number of visitors at school today (i.e. parents, builders, etc). 

The values for a, b, c, and d can all change every day, depending on how many people are at school at any particular time.  This means that the equation we have above will work every single day, no matter what. 

Now when we are dealing with algebra, it is important to understand some key words. These are in the table below. Make sure you familiarise yourself with these words. 

Now, when we work with Algebra there are a few little tricks you need to remember. The first is that when we write say "4x" this really means "4 lots of whatever x is representing" or "4 multiplied by x". We don't put in the multiplication symbol. 

Also, we rarely will write "1w" or "1g" or "1z" because what we are really saying is "1 lot of whatever symbol we choose", which in the end is just that symbol. So instead of writing "1w" we would just write "w", and the same with "1g" being just "g", or "1z" being just "z". 

Now for some examples.

If we have a certain number, a, write an expression for the following; 

• This certain number (a) increased by 7:

To do this, think of what we would do with any normal number if we wanted to increase it by 7. We would simply take this number and add 7. We use the same idea with this question here. So to increase this certain unknown number (a) by 7 we would simply add 7 to a, so an expression for this would simply be:

a + 7

• This certain number (a) decreased by 21:

Again, think of what we would do to a normal number if we were decreasing it by 21. We would simply take 21 away from the number. We use the same idea with this question here. So to decrease this certain unknown number (a) by 21 we would simply take 21 from a, so an expression for this would simply be:

a - 21

• 4 lots of this certain number (a):

Again, we think of what we would do with a normal number, which would be to multiply 4 by this number. We do this with our certain unknown number (a). We would get the expression:

4 x a

Which we know we write as:

4a

• Increase a certain number (a) by 5 then decrease the result by 7:

This is a two stage problem. First we would increase a by 5 and get the expression:

a + 5

Next, we need to decrease this by 7, or subtract 7 from this. This gives us:

a + 5 - 7

Which we can simplify (i.e. solve 5 - 7) and write as:

a - 2

Hopefully this gives you an introduction into what algebra is and the basics of how we use it. I have uploaded a worksheet on this into the "Worksheets" tab. Work through this sheet, checking your answers as you go. 

If you do have any questions on this, feel free to comment on this post, or email or chat to me in person. 

Term Break

Congratulations on completing 75% of your first year of high school. I hope you all have a fantastic and safe time off and come back feeling refreshed and ready to smash out this last term.

The plan for the final term of the year will be to start with Algebra, and then finish off spending some time looking at Statistics and Probability.

Adding and subtracting negative numbers

Today we had a look at how we add or subtract negative numbers. I found a webpage which I think explains it better than I ever could, so I suggest look at the examples on this page and how they explain it. They are very thorough and use easy-to-understand language. The website is:

http://www.mathsisfun.com/positive-negative-integers.html

In general, always remember that if:

• your signs are the same (i.e. + +, or - - ) we add
• your signs are different (i.e. + - , or - + ) we take away, or subtract. 

Your should now have the skills to finish off the worksheet. This needs to be completed by the end of the lesson on Thursday. Any incomplete work will decrease your mark overall on this unit. 

As always, if you do have any questions or concerns feel free to comment on this post, or email or chat to me in person. 

Addition, Subtraction, Multiplication, and Division

Today we had a look at adding, subtracting, multiplying, and dividing larger numbers. This should be covered in primary school, however if you need a refresher on any of these, the following websites are really handy.

Addition: http://www.mathsisfun.com/numbers/addition-column.html -> Look at the examples, clicking play to see how they work these out

Subtraction: http://www.mathsisfun.com/numbers/subtraction-regrouping.html -> Look at the examples, clicking play to see how they work these out

Multiplication: http://www.mathsisfun.com/numbers/multiplication-long.html -> Look at the examples, clicking play to see how they work these out

Division: When we are doing division, I don't want you to write an answer with a remainder. I want you to write it with decimals. Most of these examples show you how to do these.
http://www.wikihow.com/Do-Short-Division -> A good step by step method, although it does end with remainders.
http://www.youtube.com/watch?v=2X0Cjy7oEgw -> Starts by writing with remainder, however the last example does show how to calculate with decimals.
http://www.youtube.com/watch?v=PX6ktbFIKdM -> A short but good example showing a division problem with a decimal answer.

Continue to work through the worksheet.

If you do have any questions feel free to comment on this post, or email or chat to me in person.

Powers and Roots, and BODMAS

Today in class we had a look at what a power and a root are.

First we looked at powers. Now you may have seen something that looks kind of like this before:

5²

This just looks like a number 5 with a small number 2 on the right hand side of it. In maths, when we see something like this we say "five raised to the power of two". What this basically means is we want to multiply 5 by itself two times. So: 5 x 5 = 25

Now we could have something different, such as 6⁵

We say this one as "six raised to the power of five", and it simply means 6 multiplied by itself 5 times. So: 6 x 6 x 6 x 6 x 6 = 7776

Now we also have stuff that looks like this: 

In maths, we say this as the "square root of twenty-five". What this is basically asking us for is a number, that when multiplied by itself twice (because of the little two on the left) will equal 25. So in this case, we know 5 x 5 = 25, or 5 multiplied by itself twice is equal to 25, so the answer to our problem is 5. 

We could also get something that looks like this:

We can describe this one as the "third root of 64". In simpler terms, this is asking us what number, multiplied by itself 3 times, is equal to 64. We can work out that 4 x 4 x 4 = 64, or 4 multiplied by itself three times is equal to 64. So the answer to our problem is 4. 

Now finally today we had a look at order of operations. In maths, when we are faced with a problem we must solve it in a particular order. This is where order of operations comes in. A good acronym to remember is BODMAS. This stands for: 

Now we use this because it actually tells us the order we need to solve our problems. We must first solve any brackets, then followed by any Orders (basically what we were looking at above, so powers and roots). Next we solve any Division or Multiplication. These may be written as separate words, but they are really grouped together. Finally, we solve any Addition or Subtraction. Again, these are written separately but they are actually grouped together. 

The following website has some great examples. It does use a slightly different acronym (PEMDAS), however it is all the same in the end. 

http://www.mathsisfun.com/operation-order-pemdas.html 

For homework, continue working through the sheet. Remember this needs to be finished before the end of term. 

As always, feel free to comment on here if you have any questions, or email or chat to me in person.  

New Unit - Number Studies

We are now looking at a new unit for the rest of this term. It will just be a quick unit on numbers and how we use these. It is quite an important unit, as it provides the foundations for a lot of other maths and maths skills we use in the future.

The first things we looked at today was recapping on multiples and factors. We looked at these during our unit on fractions, however if you do need some reminding, this website is really handy:
http://www.mathsisfun.com/numbers/factors-multiples.html

We then had a chat about prime numbers and composite numbers. A prime number is a number that has only 2 factors, 1 and itself. A composite number is a number that has more that 2 factors.

Finally we had a look at factor trees. A factor tree is basically a way of visualising all of the prime factors of a number. We start with the number itself, then split this into a pair of factors. We then split each of these into pairs of factors, and so on until we are left with just prime number (which cannot be split any further). An example could be:

This shows 3 different factor trees of the number 108. You can see that each factor tree always finishes with the same set of numbers (in green). These numbers are the prime factors of 108. If we multiply all of these numbers together you will get your original number (in this case, 108). 

The work for this can be found under the "Worksheets" tab. It is one 5 page booklet that will last you for this whole unit. You should now be able to do most of the first page and a half. If you do know how to do more of the content, keep going with it. If not, we will look at some more stuff on this unit on Tuesday. 

As always, if you do have any questions feel free to comment on this post, or email or chat to me in person. 

Riddle 4

Create a number using only the digits 4,4,3,3,2,2,1 and 1. It can only be eight digits. You have to make sure the ones are separated by one digit, the twos are separated by two digits the threes are separated with three digits and the fours are separated by four digits. 

As always, have fun with this. Do not Google the answer. Try it for yourself. Have fun with it. If you cannot get it, don't worry.

The answer will be revealed in class on Tuesday. If you come up with a solution before then, let me know, but do not share it with others. Let them solve it themselves. 

Review of Measurement + Test

Today we started some revision of the unit of measurement. I have made a worksheet, which can be found in the "Worksheets" tab. This worksheet has a brief summary of our unit, followed by some revision questions with answers. Work through these as practice for the test.

We will be having a test on this topic on Tuesday the 8th of August. You will be allowed calculators for the whole test, and an A5 single sided information sheet. The test will be on the topics of:

• Converting between units of measurement (i.e. converting cm to m) 
• Finding perimeters of shapes
• Finding areas of shapes
• Finding volumes of 3D shapes

As always, feel free to comment on this post, or email or chat to me in person. 

Riddle number 3 answer

The answer to riddle number 3 is:

4 + 5 = 3²

Congratulation to Ruben and Indy for solving this one. 

Riddle 3

For this riddle, I need you to use the following to create a true mathematical equation.

2  3  4  5  +  =

You may only use each of those once, and it must be true. I am sure some of you are thinking, well what about:

2 + 5 = 3 + 4

But we cannot do this, because we are only allowed to use "+" once. You may combine the numbers, so take the "2" and the "3" and make "23". 

Again, it is a fun riddle, so try and solve it yourself. Do not Google it, have fun with it. 

I will be publishing the answer on Thursday. If you come up with a solution to this before then, keep it to yourself and let me know on Thursday. 

Answer to Riddle 2

The answer to the second riddle is as follows:

I would put my straight line on the '+' sign, making it a 4. This gives me a sum of 545 + 5 = 550, which is true. 

Again, congratulation to Ebony for solving this one. 

Volume of 3D shapes

Today we had a look at calculating the volume of 3D shapes. The general formula for finding the volume of a shape is:

Volume = Area of a Face x Depth (or Height)
or more generally, V = A x D

Now we know how to calculate the area of basic shapes, using the formulas in this table:

We can use these formulas to calculate the area of the face of our 3D shape. When we pick which face to calculate, we need to pick the face that has a constant profile throughout the shape. We need to pick the face so that if we were to cut the shape and take a cross section, the face would be the same dimensions, no matter where we cut it.

For example, take the following prism.

If we wanted to find the volume of this, we would pick the triangle as our face, because at any point along this prism, we will always have that triangular cross section. We would not pick one of the rectangular faces, because they are not a constant cross section throughout the shape. 

Once we know the area of the triangular face, we simply multiply this by the depth of the prism and we will have the volume. 

Another example could be this pentagonal prism:

We would pick the pentagonal face as our face to use, since at any point along the shape it will still have this as a cross section. Again, once we have the area of this face, we can then multiply it by the depth of the prism and get the volume. 

So for example, find the volume of the following prism: 

First, we will find the area of the face of this prism. In this case, we will use the from face. This is a rectangle with dimensions of 10cm and 4 cm. The area of this is: 

A = 10cm x 4cm 

A = 40cm square

Now that we have the area of the face, we can simply multiply this by the depth of the shape. In this case it is 17cm deep, so we get: 

V = 40cm square x 17cm

V = 680 cubic centimeters. 

Our units for volume are cubed. For example we may have cubic millimeters, cubic centimeters, cubic meters, cubic kilometers, etc. These are written as mm³, cm³, m³, km³ , etc

One last important point is that generally when we talk about volume in the 'real world' we would use the units of milliliters (mL) or liters (L). To convert between our units that we calculate in (i.e. cubic centimeters) and these 'real world' units, we use the following conversion: 

So if a prism has a volume of 45 cubic centimeters, we know it also has a volume of 45mL. 

It is also important to remember that 1L is 1000mL. 

I have uploaded a worksheet into the "Worksheets" tab, so work through that. I need that finished by Thursday's lesson, because we will use Thursday's lesson as a revision lesson for a test coming up. 

As always, if you have any questions comment on this post, or email or chat to me in person. 

Riddle number 2

I have another riddle for you. For this one you need the following equation:

The riddle is: Add one straight line to this equation to make it true. 

Just one rule for this one, you cannot put a line through the equals sign, to make it "not equal". 

If you come up with an answer before Tuesday's lesson, let me know. Do not tell anyone else, let them try and solve it for themselves. 

Same as last time, do not try and Google the answer. That is not the point of these riddles. They are just meant to be a little bit of fun, so try and solve it. If you can't, don't stress. I will reveal the answer on Tuesday. 

Areas of Composite Shapes

Today we still looked at areas, however we were looking at the area of composite shapes. A composite shape is an irregular shape that is made up of 2 or more regular shapes stuck together (or cut out). For example:

This is a composite shape, because it is made of 2 regular shapes. It has a rectangle with a triangle stuck to the right hand side of it. We know how to find the area of a rectangle and we also know how to find the area of a triangle, so to find the total area of this shape, we find the areas of the 2 regular shapes and add these together. 

So working this out, the area of a rectangle is length times width, so the area of this rectangle is       12 x 14 = 168 centimeters square. The area of a triangle is (base times height) divided by 2, so the area of this triangle is (8 x 12)/2 = 48 centimeters square. So the total area of this shape would simply be the area of the triangle plus the area of the rectangle, which would be 48 + 168 = 216 centimeters square. 

We do have some more complicated shapes. For example, we may have: 

The easiest way to do this one is to break it into 3 rectangles, and find the area of these three rectangles, then add the areas together. I would break it up like so: 

Now we need to find the area of each of the rectangles. 

First we will look at rectangle 1: The are of this one will simply be 12 x 4 = 48 meters square. 

Now looking at rectangle 2: This one is a little more complicated. We are told one of the side lengths, but we don't know the other. We can work this out however. We know the whole left hand side is 12m, and we know that there is 4m above rectangle 2, and 5m below it. So this means that the total side length must be 12 - 4 - 5 = 3m. So we can now work out the area of this rectangle. It would be     5 x 3 = 15 meters square. 

Finally rectangle 3: This one is a little easier. We know the height is 12m and the width is 3m so the area will be 12 x 3 = 36 meters square. 

Now that we know all the area of all of our rectangles, we can find the area of the whole shape. This will be 48 + 15 + 36 = 99 meters square. 

You should now be able to work through the rest of the worksheet on area. Try and have all of this finished by Tuesday. Remember to do all of the questions on this sheet. 

As always, feel free to comment on here if you have any questions, or email or chat to me in person. 

Riddle Answer

The answer to the riddle involved thinking a little outside the box. If you use the number 5 three times with a plus sign you can make it equal to 60. You would do it like so:

Congratulations to Ebony for getting the answer.  Well done!

Riddle

On a side note, I did give the students in the class a riddle. If I have the following:

In essence I have 3 identical numbers (20) and a plus sign (+) and I have made it equal 60. I want you to find me a sum that uses 3 different identical numbers (so not 20) and a single plus sign (+) and make it also equal to 60. I will reveal the answer in class tomorrow, so if you can come up with a solution by then, let me know before the start of class. 

Do not try and Google the answer, that would just be cheating yourself! Have a bit of fun with it, and if you can't see an answer don't stress too much. 

There may be a prize in it for anyone who gets the answer before class on Friday 27/08/2015 (i.e. before 10am) 

Area of a Shapes

So today we had a look at finding the area of a shape. The area of a shape is the total space a shape takes up. The units we use are slightly different to the units we use for length. When we measure lengths or perimeters we are just measuring those in meters, or centimeters, or millimeters, or kilometers, or others. When we are finding areas we find them in units such as meters squared, or centimeters squared, or millimeters squared, or others. These can be written like so:

The little "2" stands for "squared". 

There is one other special unit of measurement used when finding areas. This is a hectare (often written as just "ha"). This is often used for giving the area of land. One hectare is 10000 meters squared. 

Now to actually find the area of shapes, we use special formulas depending on what shape we have. I have made a nice table for you to use which shows you how to find the areas of the shapes we need to find in this unit. It looks like this:

The three shapes we really have to know how to find areas for in this unit are rectangles, parallelograms, and triangles. Now it is important to remember that a square is a special type of rectangle, where the length and width are the same. We do use the same formula for this though (length x width) 

The table above gives us all the information we need for finding the area of the shapes we need. One last point that I need to stress is the fact that you will need to make sure your units are the same. For example, if you had a rectangle with a length of 2.7m and a width of 35cm, you would have to make sure these are both either centimeters or meters. You can do either, but if the question asks you for your answer in square meters, it would make sense to convert the 35cm into meters, so your answer is in square meters. 

I have uploaded a new worksheet (as well as answers for this worksheet) in the "Worksheets" tab. You should be able to work through all of these questions in the next few days. Remember I have cut some questions out, so do all of the questions on the sheet. 

As always, if you have any questions feel free to comment on this post, or email or chat to me in person. 

  

Perimeter

Today we had a look at calculating the perimeters of shapes. The perimeter of a shape is the total distance around the shape. So for example, if we have a shape like this, the perimeter would be found by just adding the sides together. We would get:

120m + 27.5m + 60m + 32m + 36m + 35.5m = 311m 

One other key piece of information when calculating perimeters is understanding what these dashes on the sides of shapes mean

If sides have these dashes, it means they are the same length. So any side with a single dash on it is the same length as the other sides with a single dash. So for example; 

Each side with a dash on this shape (so all of them) is 18.5cm long. 

Some shapes can have some sides with one dash, and some sides with 2 or more dashes. Only the sides with the same number of dashes are of equal length. So for example:

This shape has 2 sides with a single dash, so these would both be 140cm long. It also has 2 sides with two dashes, so these would both be 6.7m long. 

There is a perimeter worksheet in the "Worksheets" tab. Do all questions on this sheet, and check your answers as you go. I have cut any irrelevant questions out, so you should be able to get this done before Thursday the 27th August. 

As always, feel free to comment on this post if you have any questions, or email or chat to me in person. 

New unit - Measurement

Today we started a new unit on measurement. This involves firstly reminding ourselves how we convert between the units we use when measuring lengths (i.e. meters, centimeters, millimeters, kilometers). Once we have mastered this, we will go on to calculate the perimeter and area's of shapes, as well as the volume of prisms.

To start with, we will look at converting between units of length. First of all, we have to remind ourselves of the difference between each. We need to remember that:

• 1 kilometer is 1000 meters
• 1 meter is 100 centimeters
• 1 centimeter is 10 millimeters

Now to convert between each, the following diagram is really helpful:

Because there are 1000 meters in a kilometer, if we wanted to find out how many meters 3 kilometers were, we would multiply the 3 by 1000, as the diagram says. The diagram also shows us how to convert between many different units. It is important to remember that km is short for kilometers, m is short for meters, cm is short for centimeters, and mm is short for millimeters. 

I have uploaded a worksheet into the "Worksheets" tab. I have circled the questions I would like you to do. If you use this diagram, this worksheet should be quite easy to complete, so simply finish off this sheet for homework by Thursday. 

As always, feel free to comment on this post if you have any questions on this topic, or email me or chat to me in person. 

Test Reminder

Just a reminder about the test tomorrow (Friday the 13 August). This will be on percentages and decimals. You will need a calculator and a pen/pencil. You are also allowed to bring in 1 A5 information sheet, with any information or examples that you may need (a good idea would be to put how to convert between percentages, decimals and fractions on there).

If you want some last minute revision, work through the questions from the chapter review. The relevant questions are listed in one of the posts below.

As always, if you have any questions feel free to comment on this post, or email or chat to me in person.

Test revision

We are at the end of our unit on percentages and decimals. This means it is time for a test. We will be having the test on Friday the 14th of August. For revision, you have a "Chapter Review" in your booklets. Work through the following questions from this:
(Ignore the "Fill in the blanks" section, skip straight through to the questions under the heading "Fluency")

2, 3, 5, 7, 9,
11 a, c,
12 a, c,
13 a, c, e
14 a, c, e
15 a, c, g, i
16 a, c
17 a, c, e
18 a, c
19 a, c
20, 23, 24, 25, 28

These do seem like a lot of questions, however this is work for all of Tuesday's lesson, as well as Thursday's lesson, and homework for the week.


As far as the test goes, you will be allowed to bring in an information sheet. This must be A5 in size and only single sided. On this, you may include any information or examples you think you may use. You will also be able to use a calculator for part on the test, so be sure to bring one of these.

As always, if you have any questions feel free to comment on here, or email or chat to me in person.

Finishing Percentages and Decimals

We are now at the end of our unit on percentages and decimals. To finish off all the unit work, please complete the following work from section 4.8 in your booklets.
1 - a, b, d, e, g, h,
2 - a, c, e, g, i
6, 7, 9, 10
13 - a) i, iii, v
14
Extension: 17

Some of this was set for homework on Tuesday, however if you haven't finished that yet finish it as well as the extra work from 4.8 for homework before our next lesson on Tuesday.

Because we are nearing the end, we will be having a test some time next week. We will discuss this in class on Tuesday. Tuesday's lesson will be dedicated to revision, looking at the chapter review at the end of your booklet.

Working With Percentages

We see percentages every day. We may see percentages on our food labels.

We also see them in news reports when we are given statistics

We are also faced with them when we are shopping

Because we see these quite often, it is essential that we know how to work with these. 

One example that we may face could be finding a percentage of a value. For example, trying to find 10% of $820. 

To do this, or first step is to convert the percentage to a decimal. In this example, 10% becomes 0.1

We then simply multiply this decimal by our whole value. So in this example, we multiply 0.1 by $820. 

This gives us a final answer of $82. So 10% of $820 is $82. 

Another example could be finding the percentage in a group. An example of this could be to find the percentage of students with brown hair if 12 out of 30 students in a class have brown hair. 

Our first step should be to make a fraction. We know from our units on fractions that 12 out of 30 can be written as a fraction 12/30. 

We then use our skills to convert a fraction to a percentage. When we do this we get 40%. 

So we know that if 12 out of 30 students have brown hair, 40% of the class have brown hair. 

Finally, another example could be when we see an item in a store reduced by a percentage. For example, we may see a pair of jeans originally priced at $80 but are then reduced by 20%. To work their reduced price, we find what 20% of $80 is, and then subtract this from the original price. 

So first we find out what 20% of $80. To do this, we multiply 0.2 by $80 and get $16. We now know that we are reducing the jeans by $80. 

Next, we subtract the $16 from the $80 and get $64. 

We now know that jeans originally marked at $80, but then reduced by 20% would cost you $64. 

You now have the skills to move onto section 4.8 of your work booklet. The questions I need you to do are:

1: a, b, d, e, g, h

2: a, c, e, g, i

6, 7, 9

If you finish these and would like to move onto some more work, look at questions 10 as well as 13, part a, questions i, iii, and v.

As always, if you have questions please feel free to comment on here, or email me or chat to me in person.  

Percentages, Decimals, and Fractions

Today we will be looking at how decimals, percentages, and fractions relate to one another.

We have spent a lot of time looking at decimals and fractions, but percentages are new to us. The word "percent" comes from the latin word "percentum", with centum meaning 100 (i.e. century is 100). So really "percent" means "per 100" or parts per 100. It is represented by the symbol %. To break this down, if we have a room with 100 students, and 12 of these students have birthdays in June, we can say that 12 out of the 100 have birthdays in June. We can say this even simpler, stating that 12 percent of the students have birthdays in June.

Still looking at percentages, if we say 80%, what we really mean is 80 parts out of 100. So for example, if 80% of teachers at Taroona High School drive a car to school, we know that 80 out of every 100 teachers drive a car to school.

Now, since we know percent means per 100, we can think "divide 100" instead. So if we wanted to write 35% and a fraction, we could just divide by 100 or make a fraction with 100 as the denominator. So 35% would be 35/100, which we can easily simplify down to 7/20, using our skills from our unit on fractions (if you need a reminder on this: http://www.mathsisfun.com/simplifying-fractions.html).
For more reading on percentages, this link is really good: http://www.mathsisfun.com/percentage.html


The main skill you need to take from today's lesson is the ability to convert between fractions, decimals, and percentages. I will go through the steps for converting each.

Converting percentage to decimals
This is quite easy. All you really need to do is to divide the original percentage by 100 and you have your decimal.
For example: 47% to a decimal. All you would do is divide 47 by 100, giving you an answer of 0.47

Converting decimal to percentage
Again, this is quite easy. All we need to do is multiply the original decimal by 100 and you have your percentage.
For example: 0.82 to a percentage. Simply multiply 0.82 by 100, giving you an answer of 82%

Converting fractions to decimals
This is also quite simple. All that needs to be done is dividing the numerator by the denominator.

For example: 3/8 to a decimal. Divide 3 by 8, and you get 0.375, which is your answer.

Converting decimals to fractions
This is slightly more difficult. It involves a few steps. First, we need to make a fraction with the original decimal as the numerator, and the number 1 as the denominator. Once we have done this, we need to convert this decimal to a whole number by multiplying by a multiple of 10 (i.e. 10, 100, 1000, 10000, etc). We then need to multiply our denominator, 1, by this same factor of 10. Once we have done all of this, we simplify our fraction. Hopefully a few examples will help make sense of this.

Converting percentages to fractions
This is much simpler than converting the decimals to fractions. Since we know that a percentage is a part out of 100, all we need to do is to make a fraction with the percentage as the numerator and 100 as the denominator. You then need to simplify your fraction.
For example: 36% as a fraction. Set up your fraction with 36 as the numerator and 100 as the denominator. You should get 36/100. Now simplify to get 9/25

Converting fractions to percentages
This is quite simple, as long as you have followed the skills I have gone thru above. The first thing you will  need to do is to convert your fraction to a decimal, by dividing the numerator by the denominator. You then want to convert this decimal to a percentage by multiplying by 100.
For example: 6/20 as a percentage. First convert it to a decimal by dividing the numerator (6) by the denominator (20). You should get an answer of 0.3. You then want to convert this to a percentage by multiplying by 100. This will give you a final answer of 30%


For practice, look at section 4.7 of your booklet. The questions you need to do are:
1 - a, c, f, h
2 - a, c, f, h
3 - a, c, e, g, i, k
4 - a, c, f, h

If you need some extra reading to help you out, this site is really helpful and has some good examples: http://www.mathsisfun.com/decimal-fraction-percentage.html
As always, if you have any question feel free to comment on here, or email me or chat to me in person.

Thursday's Lesson

Today we spent the lesson finishing off the work on decimal division. A lot of students did not do their homework, so they should still have lots of work to go on with for homework. This work is due on Friday, as we need to move on to new work in Friday's lesson.

The work that needs to be completed is in 4.6 of your booklets. We need to be finishing off the first columns of questions 1 and 3, as well as questions 6, 7, and 9. If you would like some extension work or some practice for A and B standard questions, look at questions 17 and 18.

As always, if you need any help or have any question or comments, feel free to comment on this post, or email or chat to me in person.

Decimal Division

Today we looked at how we divide decimals. As with addition, subtraction, and multiplication, we do this in a similar way to how we would divide if we had whole numbers. For a refresher on how we do that, the following links are quite helpful.

Division: http://www.wikihow.com/Do-Short-Division#/Image:Do-Short-Division-Step-4-Version-2.jpg
http://www.mathsisfun.com/numbers/division.html
http://www.youtube.com/watch?v=2X0Cjy7oEgw

Now we looked at doing division using decimals. An example of this could be 8.942 divided by 2.

Another example could be to divide 37.14 by 5.

A final example could be to divide 4.96 by 0.02. This one is slightly more difficult, because our divisor (0.02) is not a whole number. To get around this, we can multiply both our divisor and our dividend (4.96) by a number which will make our divisor a whole number. The numbers we generally multiply by are factors of 10 (so 10, 100, 1000, 10000, etc). In this case we want to multiply both numbers by 100, because multiplying 0.02 by 100 gives us 2, which is a nice easy whole number to divide by.

Now, we multiplied by 100 when we had 0.02, because that made 0.02 a nice easy number. If however, we had a divisor of say 0.0007, we would multiply by 10000, because this would make 0.0007 a nice easy number (7) to divide by. It is very important that we multiply both our divisor and dividend by the same number. It doesn't matter what the number is, as long as we multiply both by this same number, we will always get the correct answer.

Now, for homework we are still working out of that same booklet. If you have not finished the work in section 4.5 on multiplying with decimals, complete that first. Then move onto section 4.6 which is dividing with decimals. We will be doing questions 1 and 3 (the first column only for these) as well as questions 6, 7, and 9. If you are after some harder extension problems have a look at 17 and 18. By Thursday's lesson I need all for 4.5 (Multiplying) complete as well as the first columns of questions 1 and 3 in section 4.6 (Dividing).

As always, if you have any questions feel free to comment on here, or email or chat to me in person.

Decimal Multiplication

Today we looked at decimal multiplication. Again, it is very similar to standard multiplication. If you need a refresher on this (as it should have been covered in primary school) this websites have some great information and examples.

Multiplication: http://www.mathsisfun.com/numbers/multiplication-long.html

This next website is a link to the video. Once you have watched the video you can click on the green "Practice this concept" button in the top right corner to get a few practice problems. These practice problems are great because if you are getting stuck, you can click on a "Hint" button, and it will help you out a little. The website is: http://www.khanacademy.org/math/arithmetic/multiplication-division/multi_digit_multiplication/v/multiplication-6-multiple-digit-numbers


The way I multiply decimals is slightly different compared to others I have seen, however I have found it to be quite an easy method. The first step I take is to look at the problem and count the number of numbers after the decimal points in the numbers I am multiplying. I then record this off to the side because I will use it later. Next I completely ignore all the decimals and just multiply like I normally would if they were whole numbers. When I get an answer, I then need to modify this slightly. Off to the side I have recorded the number of digits after the decimal points in my question. I recorded this, because this is the number of digits that need to be after my decimal point in my answer. I then put the decimal point back into my answer in the appropriate spot so that it has the same amount of number after the decimal point as my question did. This is then my final answer.
I understand this sounds very complicated, however hopefully I can work through a few examples and it will make a little more sense.


Clicking on any of these images will enlarge them if you are having trouble viewing these.

Example 1:

Example 2:

Example 3:

If you are still having troubles, the following website is also handy

Multiplying decimals: http://www.mathsisfun.com/multiplying-decimals.html

To practice this, look in your booklet is section 4.5 "Decimal Multiplication". I want you to do the following problems:

1 and 3 -> first columns only 

7, 8, 11

Extension: 17 and 18

Our next class for maths is on Tuesday the 28th of July. I need you all to complete the first columns of 1 and 3, and then either 7, 8, or 11 by then for homework. 

As always, if you have questions or comments feel free to comment on this post, email me, or see me in person. 

Addition and Subtraction of Decimals

Today we looked at the addition and subtraction of decimals. This is very similar to the addition and subtraction of larger number, which should have been covered in primary school. If you are struggling with this or would like a refresher, the following websites are very handy.

Addition: http://www.mathsisfun.com/numbers/addition-column.html
Subtraction: http://www.mathsisfun.com/numbers/subtraction-regrouping.html

Adding and subtracting decimals is pretty much exactly the same as adding whole numbers. The key is to keep your working and setting out neat and tidy. When you write the numbers to add, be sure to line up your decimal points. You should also fill in any blank place values with zeros. Once you have done this you can simply add or subtract as you normally would. For example:

Again, some great websites for extra information on this, as well as some more examples can be found here

Addition of decimals: http://www.mathsisfun.com/adding-decimals.html
Subtraction of decimals: http://www.mathsisfun.com/subtracting-decimals.html

As far as work goes, in class we looked at section 4.4 of our booklets. We are working through the following questions:
1 and 2 -> first column of each
4, 5, 8, 10, 11, 15
Note that questions 10, 11 and 15 are more advanced questions, however all students should be able to complete up to and including question 8. If you are missing your booklet or would like further worksheets, I have included some links to further worksheets under the "Worksheets" tab.

If you have any questions or comments regarding this topic feel free to comment on here and I will get back to you.

Welcome

Welcome to the new website for year 7 maths. The idea of this website is for you to have access to what we cover in class, even if you miss a lesson. You will be able to access worksheets and any assignments we look at throughout the year. I will also put up useful websites and other links that I think you may find helpful or interesting.
If you have any questions or suggestions for this page, you may talk to me about these at any time.
Your parents can also access this page, so they can check to see what we are covering in class and also look at any assignments or homework we have on the go.

If you ever have any questions regarding a post I put up or any content we cover in class, you can always comment on this page and I will get back to you.